1982
Mi primer encuentro con estos laberintos fue hacia 1982, cuando el laberintólogo Jean-Louis Bourgeois me mostró el juego del laberinto. Me contó que este juego está muy extendido en las culturas populares de Asia y que es muy antiguo, ya que este mismo diseño aparece en las monedas cretenses de los siglos IV-V a.C., donde simboliza el laberinto en el que se encerraba al Minotauro (de hecho, hay ejemplos muy anteriores). La leyenda cuenta que Teseo encontró la salida del laberinto siguiendo un hilo que había desenrollado de una bobina que le había regalado su amada Ariadna, por lo que una línea trazada para trazar el camino a través de un laberinto como éste suele llamarse "el hilo de Ariadna".
Poco después, visitaba la casa de David Gay, matemático de la Universidad de Arizona en Tucson. Colgada de la pared había una cesta plana, de unos 45 centímetros de diámetro, tejida con un diseño que resultó ser topológicamente idéntico al laberinto cretense. David me contó que este diseño de cesta es tradicional de los indios to'ono-otum (antiguamente "papago"), una tribu que vive actualmente en el norte de Arizona, y que los giros y vueltas del camino a través del laberinto representan acontecimientos y pruebas de la vida del héroe Iitoi que aparece en la entrada.
1983
Finalmente, unos meses más tarde, visitando a mis padres en Florida y hojeando un catálogo de Sotheby's, me llamó la atención la fotografía de una página de un manuscrito hebreo medieval (un Sefer Haftorot) que se iba a vender el 23 de junio de 1983. La fotografía mostraba este diseño:
Laberinto de un Sefer Haftorot medieval.
Haga clic para una imagen más grande.
Haga clic para una imagen mucho más grande.
Los siete muros concéntricos simbolizan las siete murallas de Jericó. Las palabras del Salmo 104, vv. 1-18, 20, 21 serpentean a lo largo del camino. En el centro está escrito "Jericó" y "La imagen de la muralla de Jericó". "El lector está como caminando''. (Gracias al profesor Robert Goldberger por la traducción.) Fotografía cortesía de Sotheby's Inc., Nueva York.
Aunque este laberinto tiene un parecido superficial con el de Creta, una comparación detallada demuestra que son bastante diferentes. El laberinto de Jericó tiene 7 niveles, mientras que el de Creta tiene 8, y la secuencia en la que se alcanzan los niveles es bastante diferente de un laberinto a otro. En ambos laberintos, el camino va directamente al nivel 3 (contando el exterior como 0), pero en el laberinto cretense, luego se desdobla a través de los niveles 2 y 1, mientras que en el laberinto de Jericó, continúa a través de los niveles 4 y 5 antes de volver a 2 y 1. Las secuencias completas de los niveles son:
Cretan 0 3 2 1 4 7 6 5 8 Jericho 0 3 4 5 2 1 6 7.
Éstas pueden interpretarse como frases musicales, dejando que 0 = Do, 1 = Re, etc. El oído detecta inmediatamente que, en la melodía cretense, la frase inicial se repite en un tono más alto; como comprendí más tarde, este laberinto puede descomponerse en el producto o apilamiento de dos copias del laberinto de cuatro niveles 03214.
Habiendo visto dos ejemplos similares pero distintos, empecé a preguntarme cuántos más podría haber. Lo primero era comprender exactamente qué tenían en común. Resulta que hay tres características que comparten y que definen una clase de laberintos que pueden investigarse matemáticamente: son los laberintos simples, alternos y de tránsito. Me interesé por el problema de determinar M(n), el número de laberintos s.a.t. distintos con n niveles.
1985-86
Por aquel entonces estaba pasando un año sabático en Italia, donde Michele Emmer, profesor de la Universidad de Roma, estaba rodando una de sus películas de Matemáticas/Arte sobre laberintos. Me invitó a aparecer en la película y hablar de los laberintos s.a.t., así que escribí un guión para mí mismo que es la base de este texto. En el guión, expliqué cómo averiguar qué permutaciones de números enteros pueden ser secuencias de nivel de laberintos de la t.a.s.. (Esto quedó fuera de la película).
1986
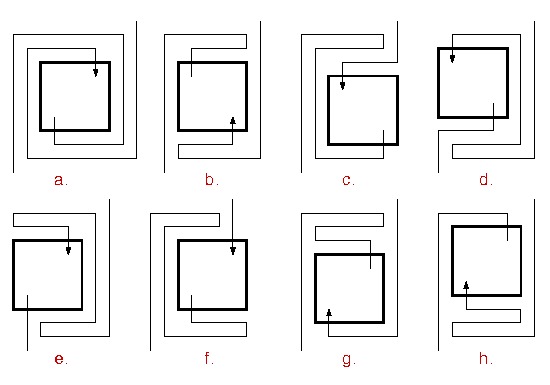
En diciembre de 1986, me encontré con Paul Erdös en una fiesta y le hablé de mi interés por este fenómeno combinatorio. Me preguntó si el número M(n) parecía aumentar exponencialmente o incluso factorialmente con n. Esta breve conversación me llevó a pensar en el comportamiento de la función M(n). Pude escribirle una semana más tarde que el número I(n) de laberintos interesantes aumenta al menos exponencialmente con n. La prueba mostraba por construcción que I(n+4)>=6I(n); el 6 puede mejorarse a 8 de la siguiente manera: para cada laberinto interesante de profundidad par n, los ocho laberintos de (n+4)--niveles mostrados aquí
Cada laberinto interesante de n niveles da lugar a 8 laberintos interesantes diferentes de profundidad n+4; en b,g,h el camino recorre el laberinto de n niveles hacia atrás.
son todos interesantes, y estos nuevos laberintos son todos distintos. En esta figura, los laberintos están representados por sus recorridos en forma rectangular. Obsérvese que el laberinto original de n niveles tiene la entrada tanto a la derecha como a la izquierda. La prueba de que estos laberintos son todos distintos requiere la hipótesis "interesante".
Entonces empecé a buscar una forma de calcular M(n). El método que había estado utilizando no era práctico para valores mayores de n, ya que implicaba considerar un número de pares de permutaciones que aumentaba, aproximadamente, como ((n/2)!)^2. Para calcular M(20), por ejemplo, sería necesario examinar unos 10^(13) pares, lo que llevaría mucho tiempo incluso en un ordenador muy rápido. La ayuda llegó de una fuente inesperada.
1987
En la sección de Ciencia del New York Times del martes 27 de enero de 1987 aparecía un artículo de James Gleick sobre el matemático Neil J. A. Sloane, que comenzaba así: "Sin proponérselo, Neil J. A. Sloane se ha convertido en el centro mundial de intercambio de información sobre secuencias numéricas. Lleva la cuenta de los fáciles, como 1, 2, 4, 8, 16, 32 ..., las potencias de dos. Lleva la cuenta de las difíciles, como 1, 1, 2, 5, 14, 38, 120, 353 ..., el número de formas diferentes de doblar tiras cada vez más largas de sellos postales".
Era la primera vez que oía hablar del problema de doblar sellos, pero está claramente relacionado con el problema de contar laberintos. De hecho, cada laberinto de profundidad n da una forma de doblar una tira de n+1 sellos: poner el laberinto en forma rectangular y colocar los sellos a lo largo del recorrido del laberinto, uno en cada nivel (incluyendo 0 y n), ignorando los segmentos verticales. Pero hay una diferencia: el primer y el último sello de una tira doblada pueden tener sus bordes libres incrustados en el interior del paquete, mientras que el primer nivel (después de 0) y el último nivel (antes de n) de un camino de laberinto deben tener sus extremos libres en el exterior. Por tanto, si F(n) es el número de formas de doblar una tira de n sellos, sólo podemos concluir que M(n)<F(n+1).
El cálculo de F(n) fue realizado por John E. Koehler, S. J. para n <= 16 en un artículo publicado en 1968. Los números empiezan como arriba y llegan hasta F(16) = 4215768. Pero lo más útil fue que Koehler describió una forma de contar los pliegues de una tira de n sellos (n par) observando pares de "patrones-n", y el número de patrones-n distintos estaba disponible en forma cerrada, para n par: era el (n/2)-ésimo número catalán Cat(n/2). Los laberintos S.a.t. con n niveles admiten una enumeración similar; en este caso, los dos n-patrones deben satisfacer la condición adicional que garantiza un único camino que recorre todo el laberinto. Ahora bien, los números catalanes, aunque estén definidos con factoriales, sólo crecen exponencialmente; de hecho
k -3/2 -1/2
Cat(k) ~ 4 k pi
para k grande, una consecuencia fácil de la fórmula de Stirling. De ello se deduce que, dado que cada laberinto de n niveles corresponde a un par de n patrones, el número M(n) de laberintos de n niveles (n par) es < = Cat(n/2)^2, por lo que crece como máximo exponencialmente.
En la práctica, hay muchos menos pares de n-patrones que pares de permutaciones de n/2 elementos, y la identificación de Koehler me permitió calcular M(n) hasta n = 22 para n par comprobando todos los pares de n-patrones para la propiedad de ciclo único. Por supuesto, el tiempo de cálculo sigue aumentando exponencialmente con n. Para n = 22, el número de pares de n-patrones a examinar era Cat(11)^2 = 3455793796. Esto llevó unas 73 horas en un ordenador Sun-3. El cálculo de n = 24 llevaría aproximadamente 16 veces más tiempo, etc.
Jim Reeds, de los Laboratorios Bell, encontró un método mejor y pudo ampliar el cálculo a n = 28.
Un subproducto de mi estudio de estos patrones de laberintos fue darme cuenta de que los laberínticos de la antigüedad trabajaban combinando un número limitado de formas fundamentales. Esto me permitió sugerir cómo deberían restaurarse los laberintos de mosaico romanos parcialmente destruidos y detectar algunos ejemplos de restauración defectuosa en los ya reparados. Véase La topología de los laberintos de mosaico romanos.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Tony Phillips
Departamento de Matemáticas SUNY Stony Brook
tony at math.stonybrook.edu
12 de febrero de 1999, 14 de mayo de 2001, 6 de diciembre de 2007
Original article: https://www.math.stonybrook.edu/~tony/mazes/motivation.html